

Click to read general information about afghans


Buy a pattern
for this afghan
on the order form


DODECAGON THING
12 identical shapes can be fitted together to make a dodecagon. 24 of the same shapes can be used to make a dodecagon with twice the area.
This only works using a particular quadrilateral and some of the shapes have to be reflected.
Either dodecagon could be made at any size and used for an afghan or cushion.
Some interesting optical effects can be created by changing the placement of the colours.


Free pattern
available
on the order form


RELATED DESIGNS
TESSELLATION AFGHANS

CONSTRUCTION INFORMATION
The shapes are made individually and stitched together. They can be made to any size.
Either 12 or 24 shapes can be used to make a cushion or afghan.
The 12-

KNITTING INFORMATION
Any yarn and needles can be used. The individual pieces are fairly small and can be worked on two needles.
Any number of colours can be used to create different effects.
Some shapes have to be turned over but this does not matter in garter stitch as both sides look alike.
Scroll down for more information about
Dodecagon Thing




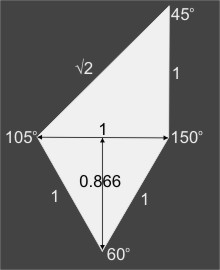
24 quadrilaterals can be arranged to create the larger dodecagon. This will only work when the ratio of the sides of the quadrilateral is 1:1:1:√2
The photograph shows one arrangement of 24 quadrilaterals.

The shapes can be arranged differently so that they can be folded over to make the back of a cushion.
This design was inspired by a presentation at a Maths conference. The presenter had been investigating shapes that could be doubled in area and still be exactly the same shape but larger.
The proof was demonstrated using two paper shapes each with a small dodecagon in the centre with ‘wings’ attached. The protruding wings were folded over to show that they completely covered the dodecagon.
The two shapes were interlocked by folding in one half of each wing to show the larger dodecagon.
The sides of the larger decagon are √2 (which is approximately 1.4) times the length of the sides of the small dodecagon.

The photos below are of the original model, which is now rather creased. The paper was red on one side and white on the other to show that the red would cover the white. The photos are not to scale.


