

Click to read general information about afghans


Buy a pattern
for this afghan
on the order form
 Buy now
Buy now


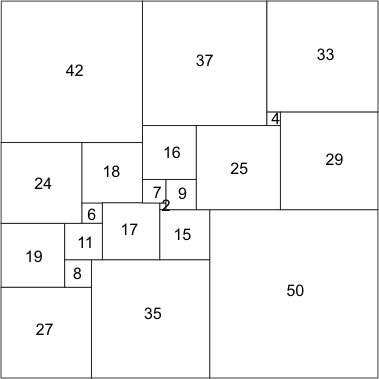
SQUARE DEAL
The design represents the smallest number of different size squares that a larger square can be split into.
The first version of Square Deal was in shades of blue and was bought for the Mathematics Collection of the Science Museum, London. The purple version was made to replace it.

The blue version was made first. It had been mounted on a board and hung in school classrooms for a couple of years until the Science Museum decided they wanted to buy it. We offered to make them a new version but they insisted on having the original.
During the time it had been hanging it had become very dusty so it was taken off the board, shaken and vacuumed. It was unceremoniously stuffed into a Sainsbury’s carrier bag and taken by train and tube to the museum’s storage building.
Getting into the building itself was an interesting experience. I had never thought about the security and fire precautions necessary to house many of the nation’s treasures in a building shared by several museums.
Once inside the fortress Square Deal and I were whisked off to the conservation department where it was handled with the same care and reverence as the most priceless item would be.

Scroll down for more information about
Square Deal

RELATED DESIGNS
NUMBER AFGHANS
CUSHION

CONSTRUCTION INFORMATION
Squares are knitted individually and stitched together.
It is also possible to knit in one piece, using several balls of yarn at a time.

KNITTING INFORMATION
Requires a minimum of 4 colours and a maximum of 21, so this could be an ideal project for using up oddments. Any type of yarn can be used.
The pattern includes instructions for making the afghan in a range of sizes.
We have a separate pattern for making it at cushion size.


For many years mathematicians had tried to solve this problem. In 1939 Roland Sprague did it using 55 squares. Nearly 40 years later, A.J.W.Duijvestjin found the solution shown here. It uses 21 different squares. No one has yet found a solution with fewer squares.
The version shown opposite was bought by the Science Museum, London, as were three other hangings. It depicts a square divided into the smallest known number of different squares which will fit together to make a square.


This photo was sent by Joan Hinchliffe of Stockport. Some of the squares were knitted by her late mother, who was then in her eighties. The afghan is now used by Joan's grand-
This is Clarabelle’s version.